As the Earth rotates on its axis from west to east, all heavenly bodies appear to rise in the east, move westwards, gaining in altitude until it is on the observer’s meridian (culminate or transit the meridian). After culmination, it continues to move westwards decreasing in altitude till it sets over the western horizon.
For a stationary observer, the interval between rising and culmination of a body will be equal to the interval between its culmination and setting, provided its
declination remains unchanged.
Also under the same circumstances, its amplitude at rising will be equal to that at setting.

When the observer is at the pole, his zenith coincides with the celestial north pole, and his rational horizon would coincide with that of equinoctial.
A celestial body with 0° declination would appear to the observer to move along his rational horizon completing a circle in exactly the same period as the Earth completes a rotation of 360 i.e. 23h 56m 04s of Mean Solar Time.
Body with ‘N’ declinations would also appear to move along a circle maintaining constant altitudes equal to their declinations. They would remain above the horizon at all times.
As the Earth rotates from W to E the celestial bodies appear to move E to W with constant altitudes and so the true altitude of the body is equal to the declination of the body and named same as the pole.
Body with ‘S’ declinations would always remain below the horizon and would not, therefore, be visible.


When the observer is on the equator, the rational horizon would be in the plane of the Earth’s axis, passing through the celestial poles.
The equinoctial and all declination circles will bisect at right angles, by his rational horizon.
All celestial bodies whether having N’ly, S’ly or 0° declination will, therefore, remain above the horizon for exactly half the day and below the horizon for the remaining half.
All bodies will rise and set perpendicular to the horizon.
When the body is on the observer’s celestial meridian, its declination is equal to (90°-True alt) and named same as the bearing of the body.
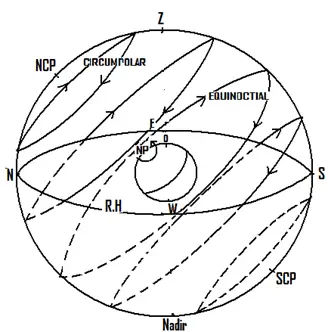
When the observer is in intermediate ‘N’ latitude, the ‘N’ celestial pole would be between the zenith and his horizon.
The RH will bisect the equinoctial at his east and west points.
A celestial body with 0° declination would be above the horizon for exactly half the day and below the horizon for the other half.
The altitude of the celestial pole is equal to the latitude of the observer As the observer’s latitude increases, the elevated pole approaches his zenith.
Therefore, a major part of the declination circles of bodies with N’ly declination (same name as latitude) would lie above the horizon and a smaller arc below it.
Bodies with N’ly declinations would, therefore, remain above the horizon for greater part of the day.
They would rise and set bearing northwards of his east and west points respectively.
If the N’ly declination of the body is large enough, its declination circle would lie entirely above the horizon. Such bodies would not, therefore, rise or set, but would remain above the horizon throughout the day. They are then said to be circumpolar.
Declination circles of bodies with a S’ly declination (of the opposite name to the observer’s latitude) will lie with a major arc of the circle below the horizon and a minor arc above. They would appear to rise and set bearing southwards of the observer’s east and west points respectively. If the S’ly declination was large enough, the declination circle would lie entirely below the horizon and the body would then not be visible during any part of the day.
Leave a Reply