The Amplitude of a body is the angle at the observer’s zenith or the arc of his rational horizon contained between the observer’s prime vertical and the vertical circle through the body, at theoretical rising or setting.
When observing the amplitude of a body, its centre should be on the rational horizon, that is, its true altitude should be exactly 0° which implies that its zenith distance will be exactly 90°.
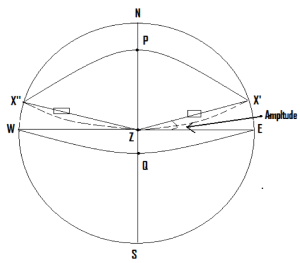 Amplitude is measured from the observer’s prime vertical, as shown in the figure, and not from the observer’s meridian.
Amplitude is measured from the observer’s prime vertical, as shown in the figure, and not from the observer’s meridian.
Amplitude is therefore named from east towards n or s when rising and from west towards n or s when setting and then converted to 360° notation.
- For a body with northerly declination, the amplitude will be northward of e or w and
- For a body with southerly declination, the amplitude will be southward of e or w
When the declination of the sun remains unchanged between rising and setting, the true amplitude at rising should equal the true amplitude at setting. Therefore sum of the true rising bearing and true setting bearing is always equal to 360°. The mean between the two bearings will therefore always be equal to 180°. The difference between 180° and the mean of the two compass bearings will therefore give the error.
Sin amplitude= sin Dec x sec lat
Using Napier’s Rule, IN QUADRANTAL SPHERICAL ∆PZX,
Sin(90-PX)=cos(90-PZ).cosZ
Sin dec = cos lat . Sin(90-Z)
Sin dec = cos lat . Sin Amp
Sin Amp = Sin dec / cos lat
Sin Amp = Sin dec . sec lat
Amplitude Calculation:
- Obtain GMT
- Obtain declination of body
- Calculate amp as per above formula
- Convert to 360° notation.
The amplitude of a rising body and also setting body will be the same for a particular declination for a stationary observer at a particular latitude in the north and also for the same value latitude in the south.

Leave a Reply